The normalized eigenfunctions for a rigid rotator that is free to rotate about its center of mass in three dimensions are the spherical harmonics
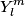 . (See Griffiths QM Problem 4.24). The given wave function can be expanded in terms of the spherical harmonics as follows . (See Griffiths QM Problem 4.24). The given wave function can be expanded in terms of the spherical harmonics as follows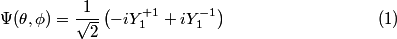 Therefore, measurement of 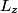 will yield m = +1 or m = -1, which corresponds to will yield m = +1 or m = -1, which corresponds to 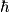 or or 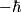 . Therefore, answer (C) is correct. . Therefore, answer (C) is correct. |